Oscilações mecânicas
Oscilações mecânicas
Na Vida diária, os
movimentos oscilatórios são bastante frequentes. São exemplos disso os
movimentos de «vaivém» de um corpo preso na extremidade de um fio,
constituindo um pêndulo de relógio, também chamado de «pêndulo gravítico
simples» (Fig. 2.1) ou o movimento de «sobe-e-desce» de um corpo de
massa m, preso na extremidade de uma mola elástica, constituindo um pêndulo
elástico (Fig. 2.2).
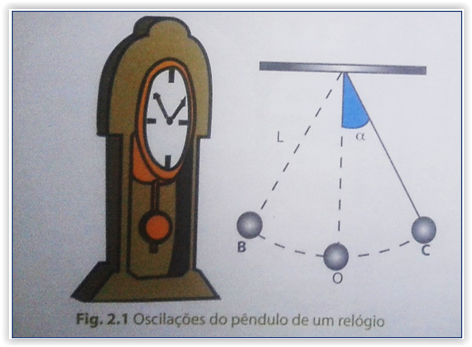 |
| Fig. 2.1: Oscilações do pendulo de um relógio. |
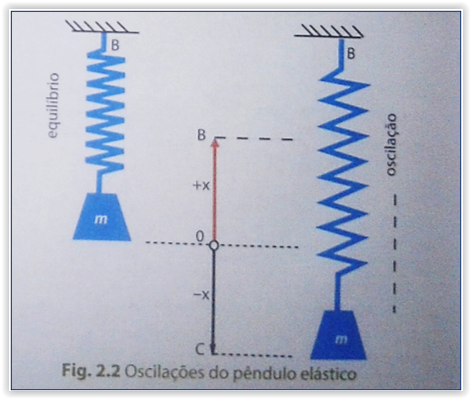 |
| Fig. 2.2: Oscilações do pendulo elástico. |
Se analisar com atenção estes dois movimentos oscilatórios, poderá verificar que:
- Os corpos oscilam entre duas posições extremas, passando pela posição de equilíbrio, isto é, o corpo oscilante, partindo do extremo B, passa pela posição de equilíbrio O, e segue em direcção extremo C. Depois repete a mesma trajectória, em sentido oposto, fazendo o trajecto C → O → B. Dizemos, então, que o oscilador realizou uma oscilação completa (movimento de vaivém).
- Após a realização da primeira oscilação, todos os parâmetros do Movimento Oscilatório repetem-se em intervalos de tempos iguais. Por isso, o Movimento Oscilatório é um movimento periódico.
Oscilações
mecânicas: são movimentos periódicos de um ponto
material, que repete sempre a mesma trajectória em sentidos opostos, em torno
de uma posição de equilíbrio, em intervalos de tempos iguais.
Características de uma oscilação mecânica
A característica
principal de uma oscilação mecânica é a sua regularidade, isto é, o intervalo
de tempo em que todos os seus parâmetros se repetem. A este intervalo de tempo,
dá-se o nome de período da oscilação (T), o qual é medido, no Sistema Internacional de
Unidades, em segundos (s). Assim:
Período
(T) de uma oscilação: é o intervalo de tempo necessário para o
corpo oscilante realizar uma oscilação completa, A sua unidade, no Sistema
Internacional, é o segundo (s).
A análise detalhada
destes osciladores, permite escrever as equações para o cálculo do período.
T
= 4. tBO ou T
= 2. tBC
Muitas vezes,
encontramos dificuldades para medir directamente o período das oscilações,
principalmente, quando são muito rápidas. O que se faz, nessas ocasiões, é
medir o número (n) de oscilações que o corpo realiza num determinado intervalo
de tempo (△t), isto é,
mede-se a frequência das oscilações. No Sistema Internacional de
Unidades a frequência é medida em hertz (Hz), em homenagem ao físico alemão do
século XVIII, Heinrich Rudolf Hertz que em 1888 provou a existência das ondas
electromagnéticas.
Frequência (f) de uma oscilação: é a grandeza física que nos indica quantas oscilações o corpo oscilante realiza na unidade de tempo. A sua unidade, no Sistema Internacional, é o hertz (Hz).
O estudo do movimento oscilatório faz-se, muitas vezes, com o auxílio do Movimento Circular Uniforme. A frequência angular ou cíclica é a grandeza física que caracteriza a rapidez com que varia o ângulo de fase (j) do movimento circular uniforme, por isso, ela é igual velocidade angular deste movimento. No Sistema Internacional de Unidades a frequência angular é medida em radiano por segundo (rad/s) e, representa-se pela letra grega óhmega (w).
Frequência
angular ou cíclica (w):
é a grandeza que caracteriza a rapidez com que varia o angulo formado pelo raio
que une o centro da circunferência ao ponto, P, em movimento circular uniforme
e um dos diâmetros das circunferências onde se projecta o ponto P.
Para além do período
(T), da frequência (f) e da frequência angular (w), há mais duas grandezas que
caracterizam o movimento oscilatório. Essas grandezas indicam a posição do
oscilador relativamente ao ponto de equilíbrio em torno do qual as oscilações
ocorrem.
Elongação: é a grandeza que nos dá a posição do oscilador, num instante qualquer, t, isto é, é o desvio momentâneo do oscilador.
Amplitude
(A): é a grandeza que nos dá a distância máxima do
oscilador, em relação à posição de equilíbrio, isto é, a amplitude é o valor da
elongação máxima.
 |
| Fig. 2.5: Elongação e amplitude. |
Transformações de energia numa oscilação mecânica
Analisemos o que ocorre, do ponto de vista energético, com as oscilações de um pêndulo gravítico simples.
 |
| Fig. 2.6: Oscilação de um pêndulo gravítico. |
Para que o pêndulo comece a oscilar devemos transportá-lo até uma das posições extremas (B ou C). Ao elevarmos o pêndulo estamos a fornecer-lhe uma certa quantidade de energia potencial, relativamente que ele possuía na posição de equilíbrio (O).
Largando o oscilador, este inicia um movimento de queda desde a posição extrema B, até à posição de equilíbrio O, quer dizer, a energia potencial fornecida em B vai sendo transformada em energia cinética do movimento do corpo oscilante que, ao passar pela posição de equilíbrio, terá a máxima velocidade possível e, consequentemente, a máxima energia cinética possível (e a mínima energia potencial).
Ao deslocar-se da posição de equilíbrio O para a posição extrema C, o sistema oscilante vai ganhando altura e perdendo velocidade. Sendo gravítico assim, o oscilador vai transformando energia cinética em energia potencial.
Atingida a posição extrema C, a energia cinética terá sido totalmente transformada em energia potencial, O oscilador realizou, então, meia oscilação.
Ao regressar para a posição de partida B, o corpo irá realizar as mesmas transformações de energia só que no sentido inverso.
Numa oscilação mecânica há uma permanente transformação de energia potencial em energia cinética e vice-versa.
Gráfico de uma oscilação
O gráfico que nos dá a posição do oscilador, em função do tempo, é uma curva ondulante, que vamos encontrar a partir de uma experiência simples.
E x p e r i ê n c i a
Determinação do gráfico de uma oscilação
Objectivo: Estudar a forma do gráfico de uma oscilação.
Material
- Um pêndulo elástico
- Um lápis
- Fita cola
- Um rolo de papel de máquina registadora
- Dois suportes cilíndricos de madeira (20 cm).
Procedimento
- Observe como o rolo de papel foi colocado nos suportes cilíndricos de madeira, de modo a poder ser enrolado pelo suporte da direita.
- Fixe, com fita cola, o lápis ao pêndulo, como ilustrado na figura.
- Coloque o rolo de papel por trás do pêndulo de modo que o lápis lhe toque levemente.
- Faça o pêndulo oscilar verticalmente e, enquanto isso, peca a um colega que, muito lentamente, vá enrolando o papel, fazendo girar o suporte da direita.
O Iápis preso ao pêndulo que sobe e desce, irá deixar no papel o gráfico que mostra a posição do corpo oscilante, em função do tempo. Poderá verificar que, esse gráfico tem a forma representada abaixo.
Nota: se não dispuser de um pêndulo elástico, pode realizar a mesma experiência usando um pêndulo gravítico simples, como ilustra a figura ao lado.
Pêndulo gravítico simples
É constituído por uma pequena partícula material que pode oscilar livremente presa na extremidade de um fio inextensível e de massa desprezável. Como analisámos anteriormente, as oscilações deste pêndulo transformam, permanentemente, energia potencial gravitacional em energia cinética e vice-versa. Mas de que factores depende o período deste pêndulo? Para respondermos a esta questão vamos realizar a seguinte experiência:
E x p e r i ê n c i a:
Determinação experimental da lei de pêndulo gravítico
Objectivo: Verificar de que factores depende o período de um pêndulo gravítico.
Material
- Fio inextensível de nylon ou crochet
- Jogo de massas diferentes
- Suporte para o pêndulo
- Fita métrica ou régua
- Cronómetro conta-segundos.
Procedimento
Faça a montagem da aparelhagem de acordo com a figura acima.
- Com a fita métrica meça o comprimento do fio que constitui o pêndulo.
- Coloque o pêndulo em oscilação e meça, com o cronómetro, o tempo necessário para o corpo realizar 10 oscilações (t10).
- Divida o tempo medido anteriormente (t10) por 10 para encontrar o período (T) das oscilações do pêndulo.
- Repita os ensaios anteriores, primeiro usando fio do mesmo comprimento e fazendo variar a massa do oscilador e, em seguida, usando a mesma massa, mas fazendo variar o comprimento do fio.
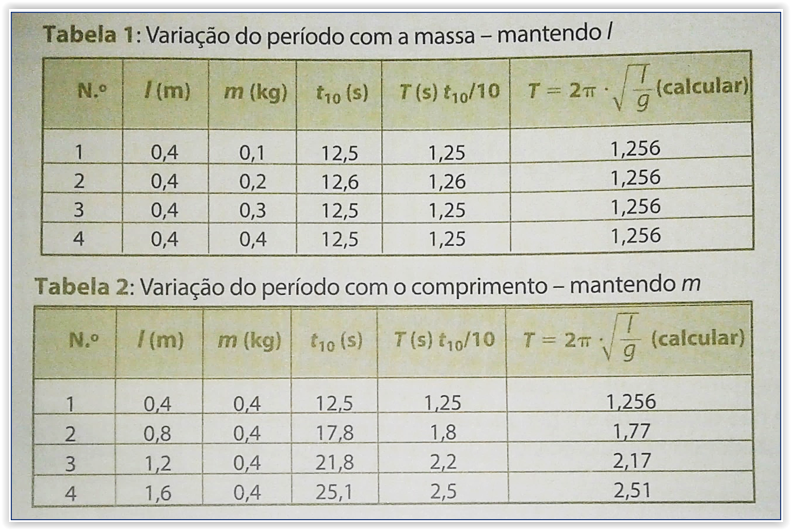
- Preencha as tabelas, como se exemplifica abaixo:
A análise dos resultados constantes nas duas tabelas permite concluir que:
a) O período de um pêndulo gravítico simples não depende da massa do oscilador: se dois pêndulos tiverem o mesmo comprimento e oscilarem no mesmo lugar, terão o mesmo período de oscilação, independentemente da massa do corpo oscilante.
b) O período de um pêndulo gravítico simples é directamente proporcional à raiz quadrada do seu comprimento: se dois pêndulos tiverem comprimentos diferentes e oscilarem no mesmo lugar, terá maior período de oscilação o pêndulo de maior comprimento.
c) O período de um pêndulo gravítico simples é inversamente proporcional à raiz quadrada da aceleração da gravidade do local onde se realizam as oscilações: nos lugares de maior aceleração da gravidade o período de oscilação é menor. Assim, por exemplo, na Terra um pêndulo oscila mais rapidamente do que na Lua porque na Terra a aceleração da gravidade é maior do que no nosso satélite.
Lei do pêndulo gravítico: para oscilações de pequena amplitude, o período de oscilação é directamente proporcional à raiz quadrada do comprimento e inversamente proporcional à raiz quadrada da aceleração da gravidade.
Onde:
- g – Aceleração da gravidade local em m/s2
- p = 3,14
- l – Comprimento do pêndulo em metros (m)
- T – Período de oscilação em segundos (s).
Pêndulo elástico
É constituído por uma partícula material de massa m, que oscila livremente presa na extremidade de uma mola elástica de constante k. Observando e analisando as oscilações de um pêndulo elástico, concluiremos que:
a) O período de oscilação do pêndulo elástico é directamente proporcional raiz quadrada da massa do oscilador: se dois pêndulos de mola tiverem a mesma constante de elasticidade K, o pêndulo que tiver maior massa terá maior período de oscilação, isto é, realizará mais lentamente as suas oscilações.
b) O período de oscilação do pêndulo elástico é inversamente proporcional à raiz quadrada da constante de elasticidade da mola: se dois pêndulos de mola tiverem a mesma massa, o pêndulo que tiver maior constante elástica terá menor período de oscilação, isto é, realizará mais rapidamente as suas oscilações.
Lei do pêndulo elástico: para oscilações de pequena amplitude, o período de oscilação é directamente proporcional ä raiz quadrada da massa do oscilador e inversamente proporcional raiz quadrada da constante elástica da mola.
Onde:
- m – Massa do oscilador em quilogramas (kg)
- p = 3,14
- k – Constante elástica da mola em N/m
- T – Período de oscilação em segundos (s).
Bibliografia
MENESES, João Paulo. F10 - Física 10ª Classe. Texto Editores, Maputo, 2017.




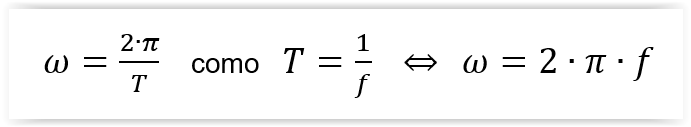









Comentários