Transformações de energia numa oscilação mecânica

Analisemos o que ocorre, do ponto de vista energético, com as oscilações de um pêndulo gravítico simples.

Fig. 2.6: Oscilação de um pêndulo gravítico.

Para que o pêndulo comece a oscilar devemos transportá-lo até uma das posições extremas (B ou C). Ao elevarmos o pêndulo estamos a fornecer-lhe uma certa quantidade de energia potencial, relativamente que ele possuía na posição de equilíbrio (O).

Largando o oscilador, este inicia um movimento de queda desde a posição extrema B, até à posição de equilíbrio O, quer dizer, a energia potencial fornecida em B vai sendo transformada em energia cinética do movimento do corpo oscilante que, ao passar pela posição de equilíbrio, terá a máxima velocidade possível e, consequentemente, a máxima energia cinética possível (e a mínima energia potencial).

Ao deslocar-se da posição de equilíbrio O para a posição extrema C, o sistema oscilante vai ganhando altura e perdendo velocidade. Sendo gravítico assim, o oscilador vai transformando energia cinética em energia potencial.

Atingida a posição extrema C, a energia cinética terá sido totalmente transformada em energia potencial, O oscilador realizou, então, meia oscilação.

Ao regressar para a posição de partida B, o corpo irá realizar as mesmas transformações de energia só que no sentido inverso.

Numa oscilação mecânica há uma permanente transformação de energia potencial em energia cinética e vice-versa.

Gráfico de uma oscilação  

O gráfico que nos dá a posição do oscilador, em função do tempo, é uma curva ondulante, que vamos encontrar a partir de uma experiência simples.

E x p e r i ê n c i a

Determinação do gráfico de uma oscilação

Objectivo: Estudar a forma do gráfico de uma oscilação.

Material

• Um pêndulo elástico
• Um lápis
• Fita cola
• Um rolo de papel de máquina registadora
• Dois suportes cilíndricos de madeira (20 cm).

Procedimento

• Observe como o rolo de papel foi colocado nos suportes cilíndricos de madeira, de modo a poder ser enrolado pelo suporte da direita.
• Fixe, com fita cola, o lápis ao pêndulo, como ilustrado na figura.
• Coloque o rolo de papel por trás do pêndulo de modo que o lápis lhe toque levemente.
• Faça o pêndulo oscilar verticalmente e, enquanto isso, peca a um colega que, muito lentamente, vá enrolando o papel, fazendo girar o suporte da direita.

O Iápis preso ao pêndulo que sobe e desce, irá deixar no papel o gráfico que mostra a posição do corpo oscilante, em função do tempo. Poderá verificar que, esse gráfico tem a forma representada abaixo.

Nota: se não dispuser de um pêndulo elástico, pode realizar a mesma experiência usando um pêndulo gravítico simples, como ilustra a figura ao lado.

Pêndulo gravítico simples

É constituído por uma pequena partícula material que pode oscilar livremente presa na extremidade de um fio inextensível e de massa desprezável. Como analisámos anteriormente, as oscilações deste pêndulo transformam, permanentemente, energia potencial gravitacional em energia cinética e vice-versa. Mas de que factores depende o período deste pêndulo? Para respondermos a esta questão vamos realizar a seguinte experiência:

E x p e r i ê n c i a:

Determinação experimental da lei de pêndulo gravítico

Objectivo: Verificar de que factores depende o período de um pêndulo gravítico.

Material

• Fio inextensível de nylon ou crochet
• Jogo de massas diferentes
• Suporte para o pêndulo
• Fita métrica ou régua
• Cronómetro conta-segundos.

Procedimento

Faça a montagem da aparelhagem de acordo com a figura acima.

• Com a fita métrica meça o comprimento do fio que constitui o pêndulo.
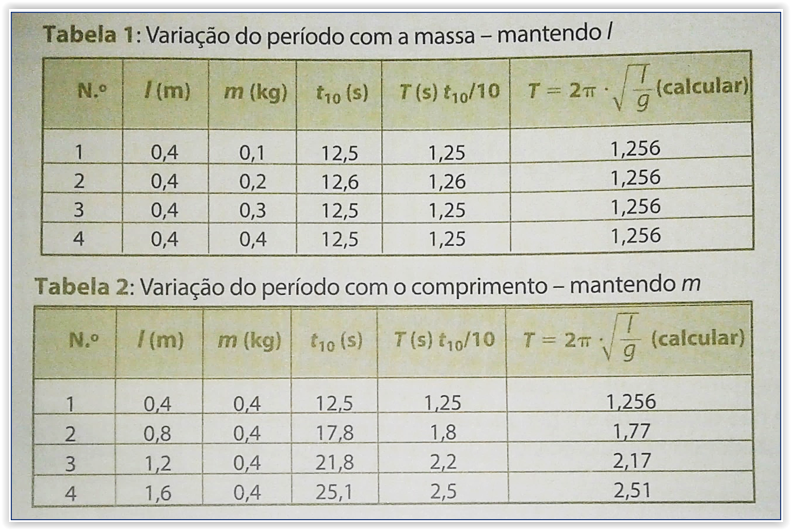
• Coloque o pêndulo em oscilação e meça, com o cronómetro, o tempo necessário para o corpo realizar 10 oscilações (t₁₀).
• Divida o tempo medido anteriormente (t₁₀) por 10 para encontrar o período (T) das oscilações do pêndulo.
• Repita os ensaios anteriores, primeiro usando fio do mesmo comprimento e fazendo variar a massa do oscilador e, em seguida, usando a mesma massa, mas fazendo variar o comprimento do fio.
• Preencha as tabelas, como se exemplifica abaixo:

A análise dos resultados constantes nas duas tabelas permite concluir que:

a) O período de um pêndulo gravítico simples não depende da massa do oscilador: se dois pêndulos tiverem o mesmo comprimento e oscilarem no mesmo lugar, terão o mesmo período de oscilação, independentemente da massa do corpo oscilante.

b) O período de um pêndulo gravítico simples é directamente proporcional à raiz quadrada do seu comprimento: se dois pêndulos tiverem comprimentos diferentes e oscilarem no mesmo lugar, terá maior período de oscilação o pêndulo de maior comprimento.

c) O período de um pêndulo gravítico simples é inversamente proporcional à raiz quadrada da aceleração da gravidade do local onde se realizam as oscilações: nos lugares de maior aceleração da gravidade o período de oscilação é menor. Assim, por exemplo, na Terra um pêndulo oscila mais rapidamente do que na Lua porque na Terra a aceleração da gravidade é maior do que no nosso satélite.

Lei do pêndulo gravítico: para oscilações de pequena amplitude, o período de oscilação é directamente proporcional à raiz quadrada do comprimento e inversamente proporcional à raiz quadrada da aceleração da gravidade.

Onde:

• g – Aceleração da gravidade local em m/s²
• p = 3,14
• l – Comprimento do pêndulo em metros (m)
• T – Período de oscilação em segundos (s).

Pêndulo elástico

É constituído por uma partícula material de massa m, que oscila livremente presa na extremidade de uma mola elástica de constante k. Observando e analisando as oscilações de um pêndulo elástico, concluiremos que:

a) O período de oscilação do pêndulo elástico é directamente proporcional raiz quadrada da massa do oscilador: se dois pêndulos de mola tiverem a mesma constante de elasticidade K, o pêndulo que tiver maior massa terá maior período de oscilação, isto é, realizará mais lentamente as suas oscilações.

b) O período de oscilação do pêndulo elástico é inversamente proporcional à raiz quadrada da constante de elasticidade da mola: se dois pêndulos de mola tiverem a mesma massa, o pêndulo que tiver maior constante elástica terá menor período de oscilação, isto é, realizará mais rapidamente as suas oscilações.

Lei do pêndulo elástico: para oscilações de pequena amplitude, o período de oscilação é directamente proporcional ä raiz quadrada da massa do oscilador e inversamente proporcional raiz quadrada da constante elástica da mola.

Onde:

• m – Massa do oscilador em quilogramas (kg)
• p = 3,14
• k – Constante elástica da mola em N/m
• T – Período de oscilação em segundos (s).

 

Bibliografia

MENESES, João Paulo. F10 - Física 10ª Classe. Texto Editores, Maputo, 2017.